間接参照とは、値そのものではなく、名前やコンテナを通じて値を参照するコンピューターの機能を説明するコンピューター プログラミングの概念です。このように名前やコンテナを通じて値が参照されることを間接参照のレベルと言います。
Optimizer では、目標と制約に使用するライン アイテムが次の三つのカテゴリーのいずれかに分けられます。
- 変数
- 変数に依存
- 変数から独立
目標または制約の式で使用する変数に依存するライン アイテムには間接参照のレベルを一つしか設定できません (一方、変数から独立している式コンポーネントには複数の間接参照のレベルを設定可能)。そのため、変数そのものであるライン アイテム、又は変数を含むライン アイテムを式で参照できますが、変数を含む別のライン アイテムを参照するライン アイテムを、式で参照することはできません。この概念を図にしたものが下記です。
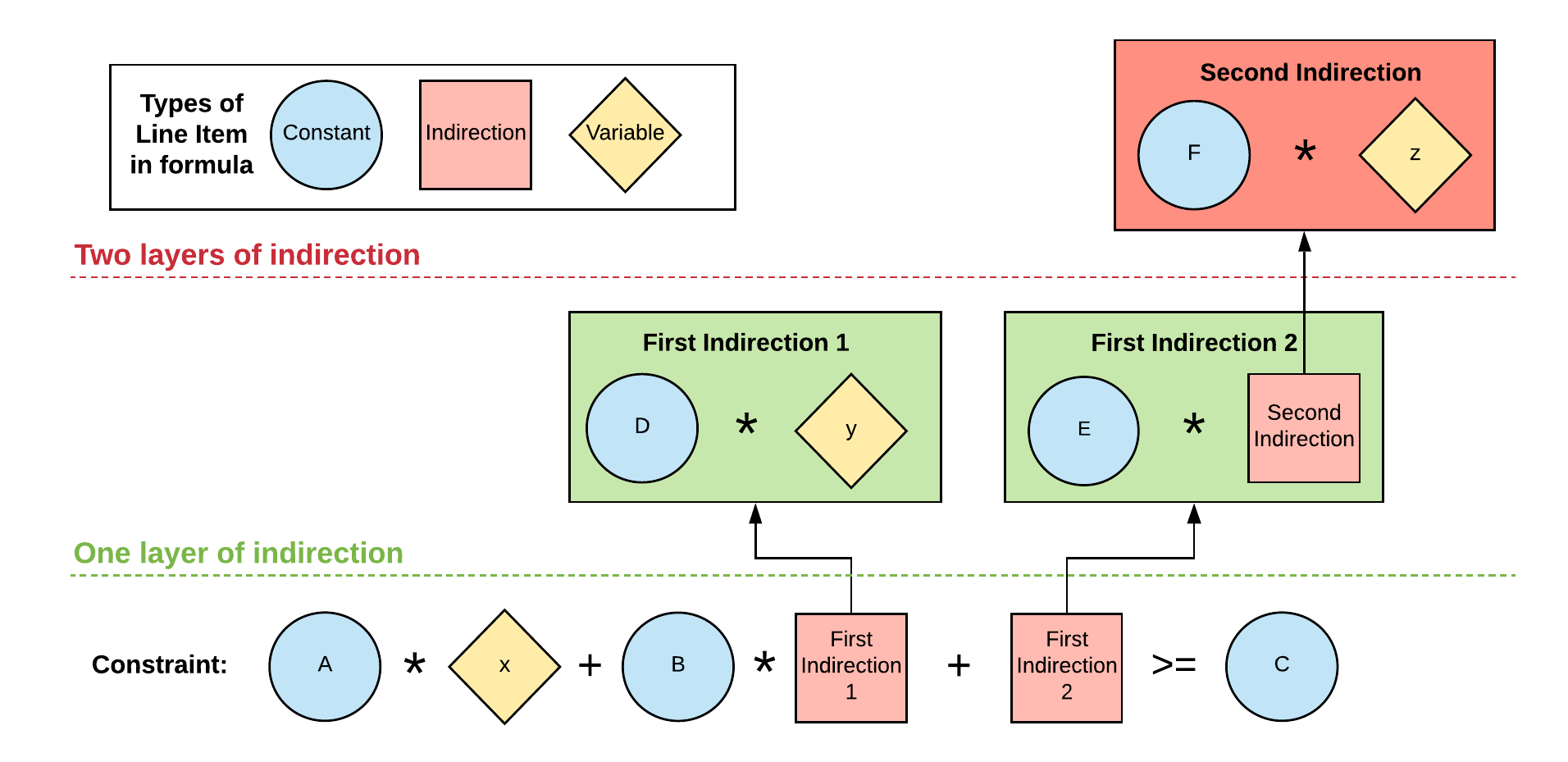
| ライン アイテム | 式 | ライン アイテムのカテゴリー |
| x | 該当なし | 変数 |
| y | 該当なし | 変数 |
| z | 該当なし | 変数 |
| A | 該当なし | 変数から独立 |
| B | 該当なし | 変数から独立 |
| C | 該当なし | 変数から独立 |
| D | 該当なし | 変数から独立 |
| E | 該当なし | 変数から独立 |
| F | 該当なし | 変数から独立 |
| G | E * F | 変数から独立した式 |
| 制約 | A * x + B * First Indirection 1 + First Indirection 2 >= C | 制約 |
| First Indirection 1 | D * y | 変数に依存する式 |
| First Indirection 2 | E * Second Indirection | 変数に依存する式 |
| Second Indirection | F * z | 変数に依存する式 |
最適化で、上記の図で制約式を使用しようとするとエラーが表示されます。例:
プロセスが失敗しました。詳細については以下をクリックしてください。
工場割り当ての最適化
アクションが失敗しました。目標「Direct Assignment Costs」が存在しません。Optimizer アクションを編集してライン アイテムを削除してください。
Optimizer では処理できない、二つのレベルの間接参照がある変数が使用されているため、目標 (又は制約) が存在しないというメッセージが表示されます。
図では、変数を使用する式を含む 2 番目のライン アイテム「Second Indirection」をライン アイテム「First Indirection 2」が参照しているため、エラーが発生しています。
最適化問題の再モデル化
最適化問題を再モデル化することで、単一の間接参照の制限を説明することができます。間接参照の最初のレベルですべての変数が直接参照されるようにしてください。最適化問題を再モデル化する手順は以下のとおりです。
- 間接参照の最初のレベルと 2 番目のレベルの式が変数をどのように操作するかを特定します。
- 変数と関連する演算子を分離し、それらの式の残りの内容を含む新しいライン アイテムを作成します。
- 間接参照の最初のレベルで新しいライン アイテムを使用し、変数と組み合わせることで変数を直接参照する新しい式を作成します。
間接参照の制限の回避策の例
間接参照の制限の回避策の例については以下の図を参照してください。
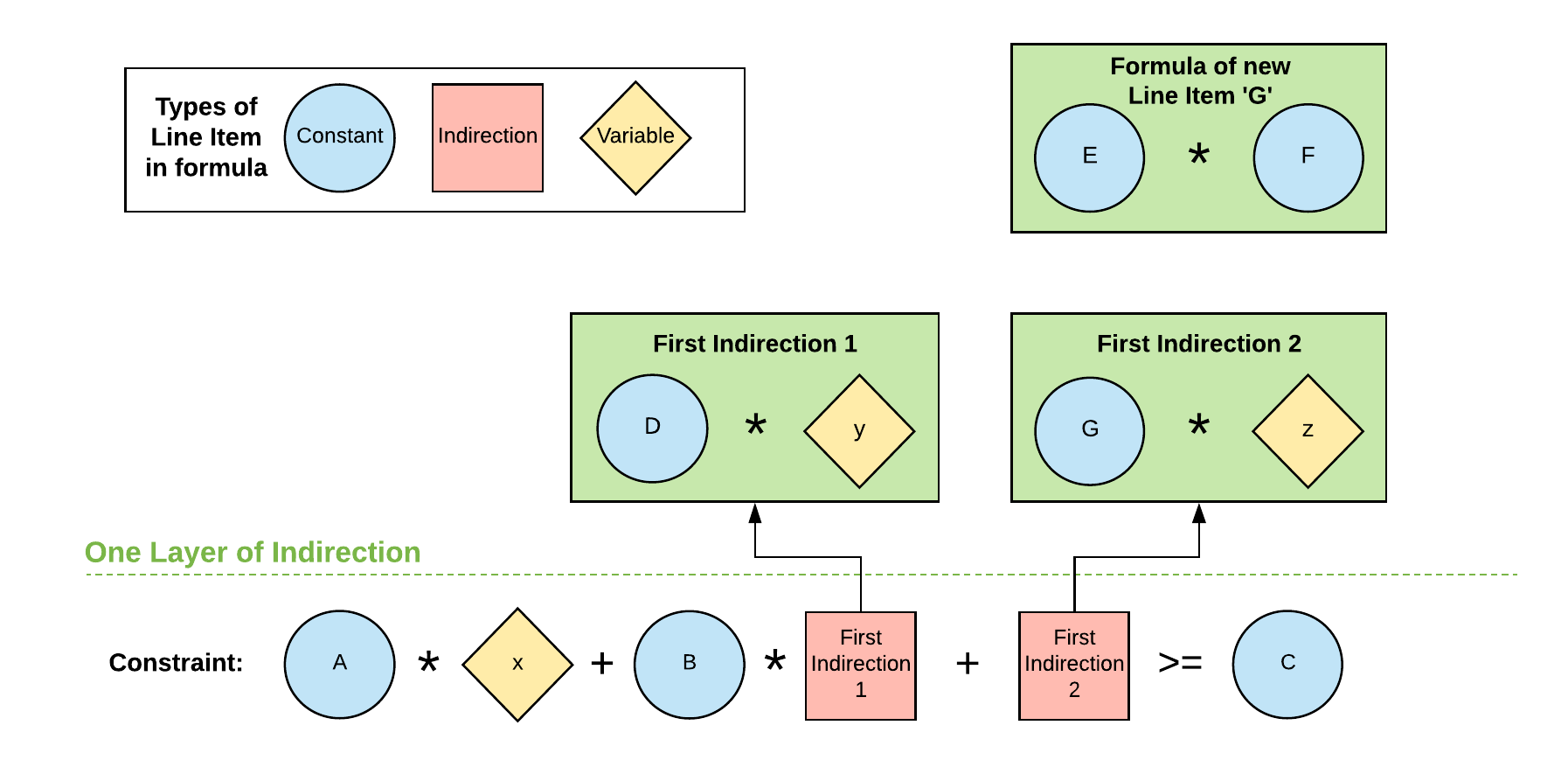
この回避策を実行する手順は以下のとおりです。
- 間接参照の問題が「Second Indirection」に起因しており、その原因の延長線上に「First Indirection 2」があることを特定します。
- これらのライン アイテムで使用されている式を確認して一つにまとめます。
E * F * z - 変数とその演算子「
* z」を分離します。 - 式の残りの部分 (
E * F) を含む新しいライン アイテム「G」を作成します。 - 新しいライン アイテム「G」を使用して「First Indirection 2」に新しい式「
G * z」を作成し、分離した変数およびその演算子を新しいライン アイテムと再度結合します。
新しいライン アイテム「G」を作成し、変数「z」で式で使用することで、間接参照の 2 番目のレベルを削除できます。これにより制約式が動作するようになり、エラーなしで最適化を実行できるようになります。

