Indirection is a computer programming concept that describes a computer's ability to reference a value through a name or container, rather than the value itself. Each time that a value is referenced through such a name or container is known as a level of indirection.
In Optimizer, the line items that you use for objectives and constraints fall into one of three categories:
- a variable
- dependent upon a variable
- are independent of variables
Any line items that are dependent upon variables that you used in your objective or constraint formulas can only have one level of indirection (although formula components that are independent of variables can have more than one level of indirection). This means that formulas can refer to line items that are a variable or that contain a variable, but they can't refer to line items that refer to another line item containing a variable. This concept is illustrated in the diagram below.
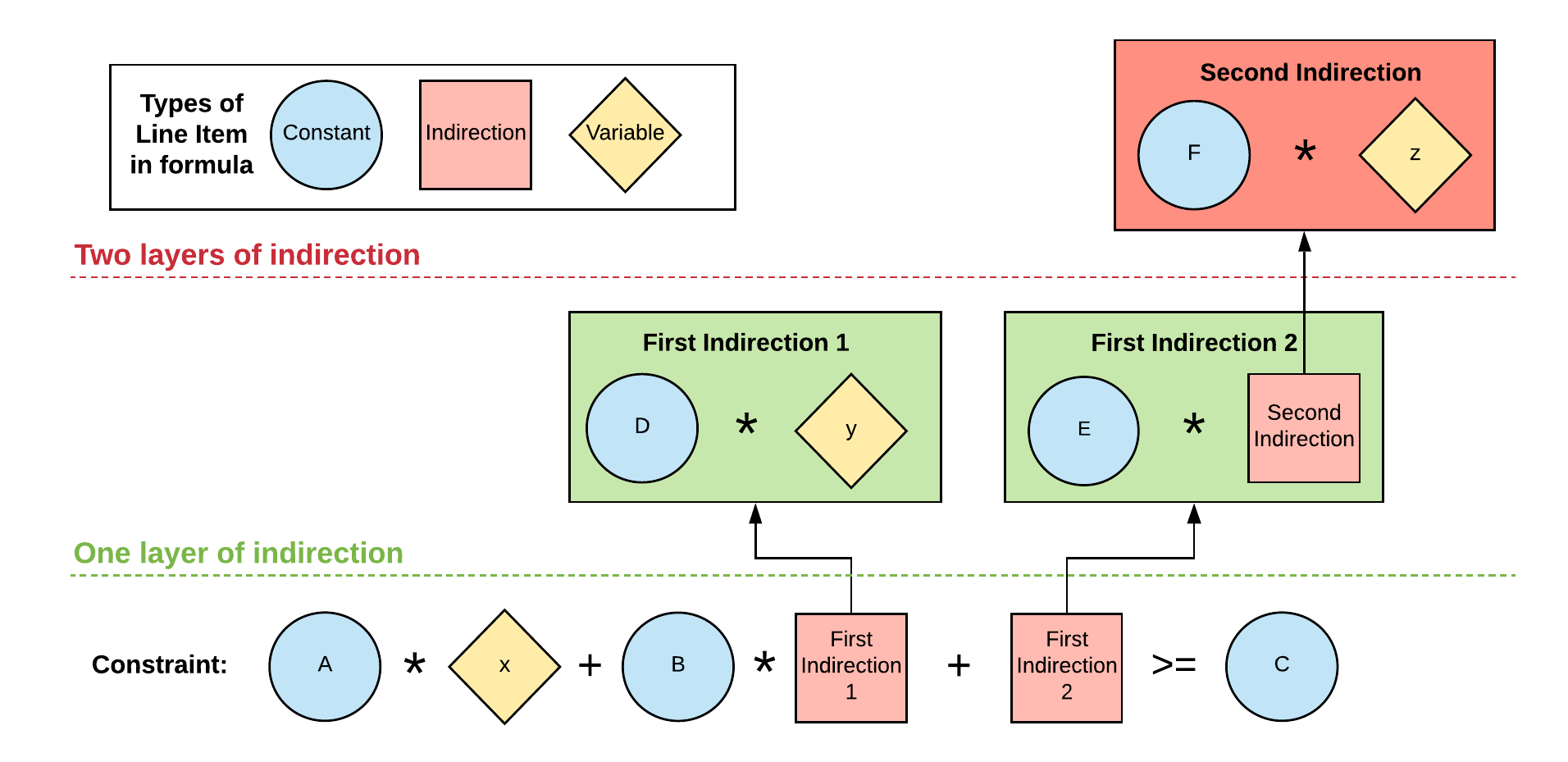
| Line item | Formula | Line item category |
| x | N/A | Variable |
| y | N/A | Variable |
| z | N/A | Variable |
| A | N/A | Independent of variables |
| B | N/A | Independent of variables |
| C | N/A | Independent of variables |
| D | N/A | Independent of variables |
| E | N/A | Independent of variables |
| F | N/A | Independent of variables |
| G | E * F | Formula independent of variables |
| Constraint | A * x + B * First Indirection 1 + First Indirection 2 >= C | Constraint |
| First Indirection 1 | D * y | Variable-dependent formula |
| First Indirection 2 | E * Second Indirection | Variable-dependent formula |
| Second Indirection | F * z | Variable-dependent formula |
If you attempt to use the constraint formula in the diagram above in an optimization, an error will be displayed. For example:
Process failed. Click below for details.
Factory Assignment Optimization
Action failed. The Objective 'Direct Assignment Costs' does not exist. Edit the Optimizer action to remove the line item.
The message states that an objective (or constraint) doesn't exist because it uses a variable with two levels of indirection, which Optimizer isn't able to process.
In the diagram, the error occurs because the line item First Indirection 2 refers to a second line item Second Indirection, which contains a formula that uses a variable.
Remodel an optimization problem
You can remodel optimization problems to account for the single indirection limitation. Make sure that any variables are referenced directly in the first level of indirection. To remodel an optimization problem, follow these steps:
- Identify how any formulas in the first and second level of indirection interact with variables.
- Isolate the variables and any attached operators; then create new line items containing the rest of the contents of these formulas.
- Use the new line items in the first level of indirection, combining them with the variables to create new formulas that directly reference the variables.
Example of working around the indirection limitation
See the diagram below for an example of how to work around the indirection limitation.
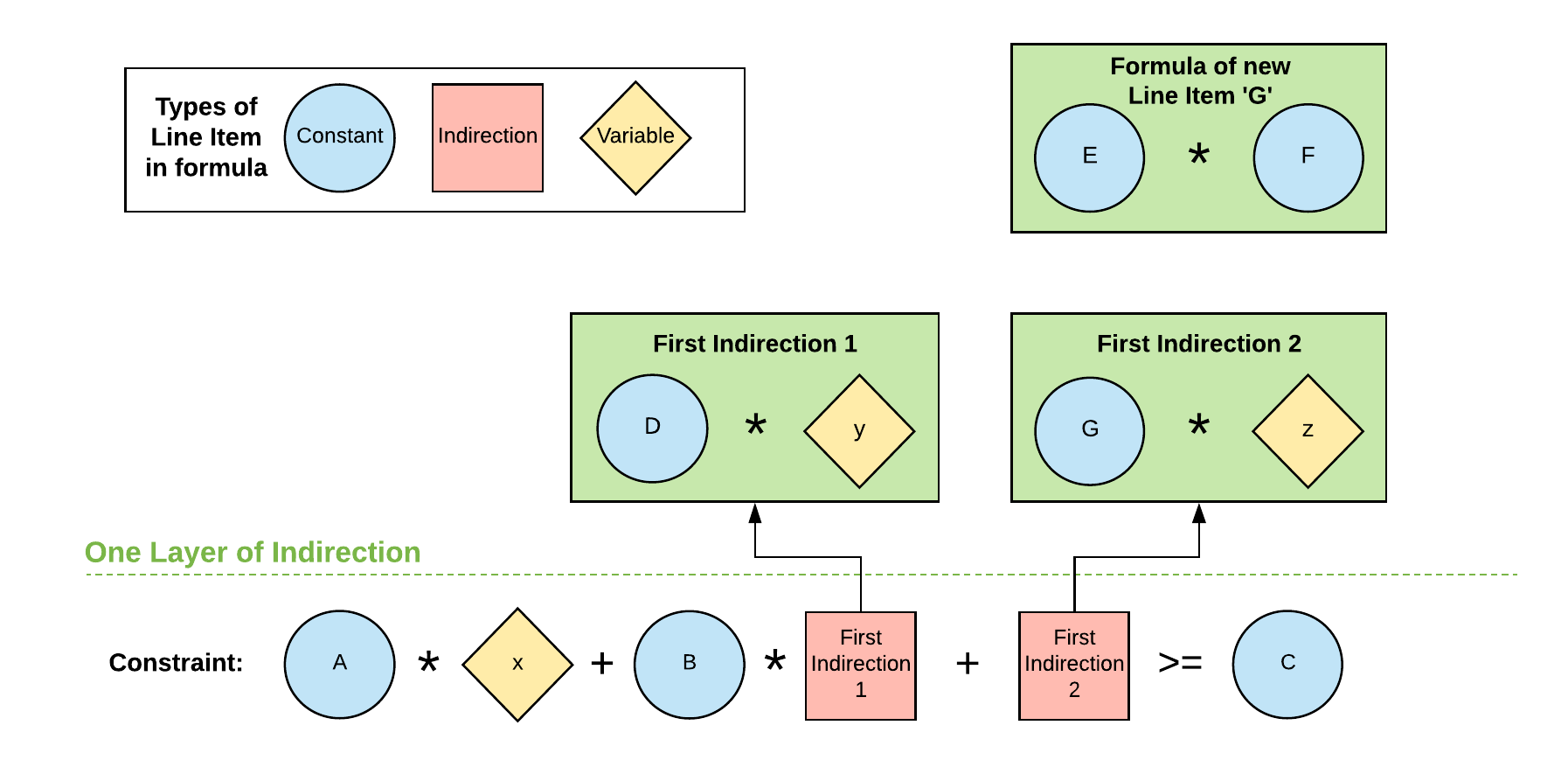
To get to this stage, follow these steps:
- Identify that the indirection problem originates in Second Indirection, and by extension First Indirection 2
- Examine the formulas used in these line items and consolidate them:
E * F * z - Isolate the variable and its operator,
* z - Create a new line item, G, that contains the remainder of the formula,
E * F - Use the new line item G to create a new formula in First Indirection 2,
G * z, recombining the new line item with the isolated variable and its operator.
By creating the new line item G and using it in a formula with the variable z, we can remove the second level of indirection. This means our constraint formula will work and the optimization can run without error.

