線形計画法とは、線形問題の解を求めるために使用する数学的概念です。通常、線形計画法の目標は指定された目標 (利益やコストなど) を最大化または最小化することです。このプロセスのことを最適化と呼びます。変数、目標、制約という三つの概念に依存しています。
変数は数値かブール値です (生産する製品の数量や、流通センターが開いているかどうかなど)。線形計画法ではこうした変数の最適値を求めます。目標 (最大利益など) は最適化の変数の線形関数です。制約も最適化の変数の線形関数で、最適化で変数に対して返せる値を制限するために使用します。制約はブール値の線形関数にする必要があります。制約の例として、予算割り当ての指定された比率や、工場で生産できる商品の合計数などが挙げられます。
チャートの観点から線形計画法を考えることで、イメージと理解がしやすくなります。目標や制約などの線形関数はグラフで直線として表示されます。変数は x と y、または未知の値と考えることができます。以下の画像は、目標と制約の線形関数をプロットすることで、線形計画または最適化が実行可能なリージョンを特定する方法を示したものです。
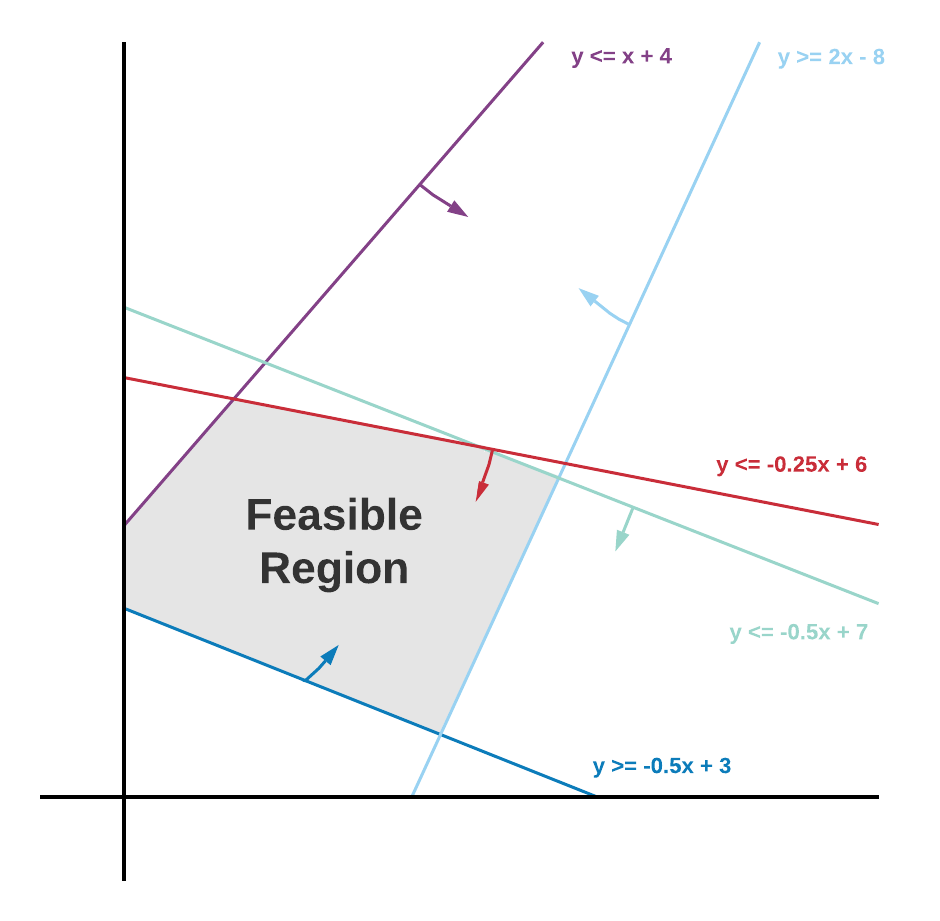
多くの場合、目標の最適値はこの実行可能なリージョンの角になります。これが目標の最大または最小の実行可能値になるためです。

