パレート分析

複合グラフを使用することで、パレートの法則をベースにした統計手法であるパレート分析を作成できます。80:20 の法則とも呼ばれるパレートの法則では、特定の状況やシステムからの出力の 80% は典型的分布の入力の 20% によって決まるとされています。

問題の原因をランク付けし、最も影響が大きい解決策に集中することで、全体の 80% の改善を達成できます。分析で洗い出した 20% の部分に取り組むことで、問題の 80% を占める部分を改善できるのです。

パレートの法則は次のようなさまざまな状況に応用できます。

• 顧客の苦情の 80% が 20% の潜在的な問題を原因としている。
• スケジュール遅れの 80% が 20% の潜在的な遅延要因に起因している。
• 20% の製品とサービスが利益全体の 80% を占めている。
• 20% の営業担当者が企業収益全体の 80% を生み出している。
• 20% のシステムの欠陥が問題の 80% の原因となっている。

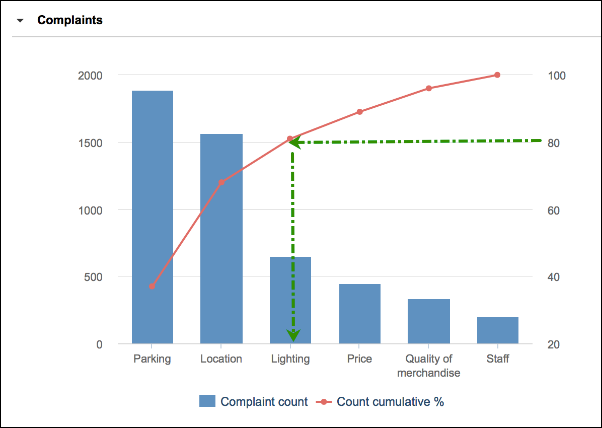
ある小売店で売上が減少しているものの、その理由がわからない場合を例にとってみましょう。その小売店では、来店するのをやめた理由を複数のカテゴリーから顧客に選択してもらうアンケートを作成しました。駐車場、店舗の場所、照明、価格、商品の品質、スタッフがカテゴリーに含まれています。

パレート分析に回答をプロットすることで、顧客に再度来店してもらうために最初に取り組むべきカテゴリーがわかります。顧客が来店しない理由として駐車場と店舗の場所が原因になっていることが結果からわかりました。80% の線が照明の中心に来るため、駐車場と店舗の場所の次に確認した方がよさそうです。

複合グラフではカテゴリーと数の値が縦棒グラフに表示され、発生頻度 (左から右) を基準に降順でランク付けされます。左側の垂直軸は通常、縦棒グラフ (カテゴリー) に関連しています。

縦棒グラフに重ねて表示される折れ線グラフには、累積値がパーセンテージで表示されます (分析結果が左から右に合計で 100% になるまで)。右側の垂直軸は折れ線グラフ (累積合計) に関連しています。

2 番目の Y 軸の 80% マーカーを起点にして、折れ線グラフの線に当たるまで線が左方向に描画されます。ここから線が X 軸方向に真下に描画されます。X 軸のこのポイントの左側にあるアイテムに対処した場合に最も高い効果が得られます。

小売店の例を使用して、パレート分析の作成に必要な手順を紹介します。

1. アンケートのカテゴリー (モジュール内の個別のカウントと累積パーセンテージのカウント) を記録します。
2. カテゴリー ライン アイテムを降順で並べ替え、ライフ アイテムのカウントが一番上に来るようにします。
3. X 軸がカテゴリー、カウントが左側の Y 軸、パーセンテージ カウントが右側の Y 軸の複合グラフを作成します。
4. 右側の Y 軸の 80% のところから左方向に水平に手動で線を描画します。
5. 折れ線グラフと当たるところで真下に向かって線を描画します。X 軸のこのポイントが左側の重要なカテゴリーと右側のそれほど重要ではないカテゴリーを分ける境界になります。